折り紙関連記事3つ目です。折り紙は、鶴や手裏剣などのように1枚で何かを創り上げる事ができますが、複数枚組み合わせたり、立体を作ったりと表現の幅が広いです。今回は「数理×折り紙」ということで科学折り紙の世界の入口に触れてみたいと思います。
折り紙の世界は広いのですが、平に折りたたまれた状態「平坦折」に絞って、角度の関係を中心にまとめています。
折り紙と数学の関係
日本人は古くから折り紙に親しみがありますが、数学的目線で見たことがある人はどのくらいいるでしょうか。もしかしたら高校で幾何学を習う際に、折り紙で実習をした人もいるかもしれませんね。
この折り紙の分野、「Origamics(オリガミクス)」という言葉が誕生し、世界の数学者達が科学折り紙に取り組んでいます。
- origamics・・・科学折り紙の一分野で、模倣作品を作る事を目的とせずに紙を折ったり重ねたりして、そこに生じる数理現象を追求すること
折り紙の角度に注目する
まず当記事で扱う折り紙は以下のものと定義しておきます。
- 正方形の紙を使用し、俗に言う「折り紙遊び」で使用する紙を想定
- 分度器・定規・コンパス・はさみ等の道具は使用しない
折り紙で鶴を折れる人は比較的多いと思います。
その際、翼の先端は45度で、クチバシは11.25度だから・・・なんて考えている人は殆どいないでしょう。
この折り紙の角度に注目すると、正三角形などの多角形が簡単に折れるんですよー。
折り紙で正三角形を折る
当記事の折り紙には正方形の紙を使用します。
つまり、各辺の長さが等しく、角度は90度。この性質を利用して正三角形を折り方をご紹介します。折り方は様々あるのですが、ここでは「内接する最大の正三角形」の折り方をご紹介します。
正三角形の特徴
まず、折りたいもの=正三角形の特徴を思い出しましょう。
- 3つの辺の長さが等しい
- 3つの角度の合計は180度=1つの角は60度
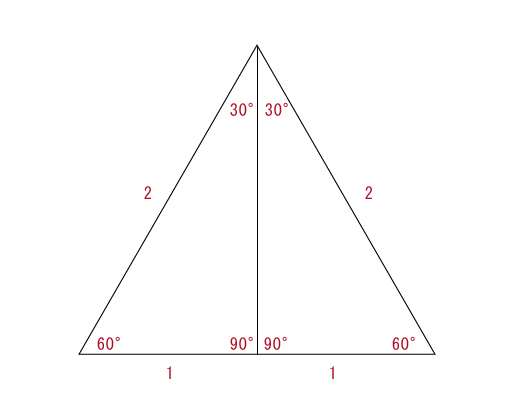
内接する最大の正三角形の折り方
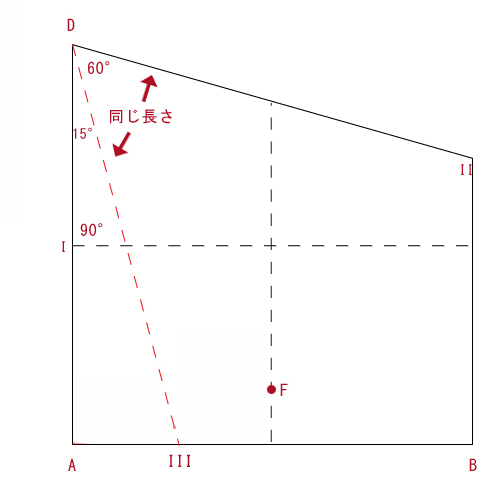
正三角形は2つの直角三角形に分割できる事を利用して作成します。
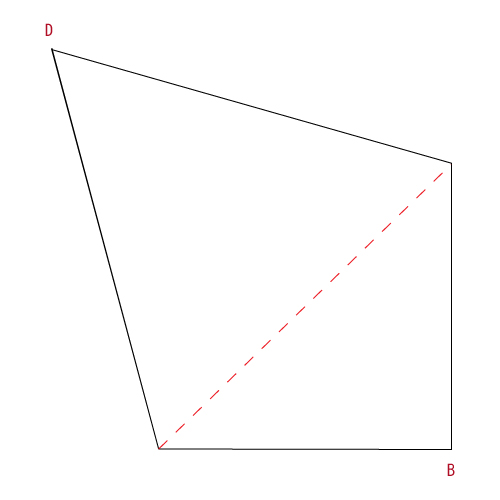
- 縦横それぞれ中央で折って折り目を付ける。
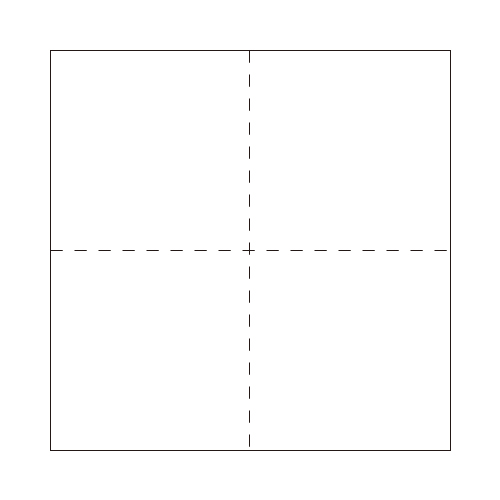
- 頂点Dを軸として、頂点Cを横断線に重ねるように折る。
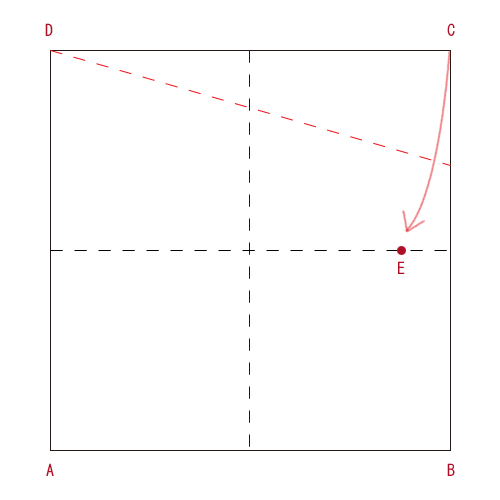
- 頂点Dを軸として、頂点Aを縦断線に重ねるように折る。
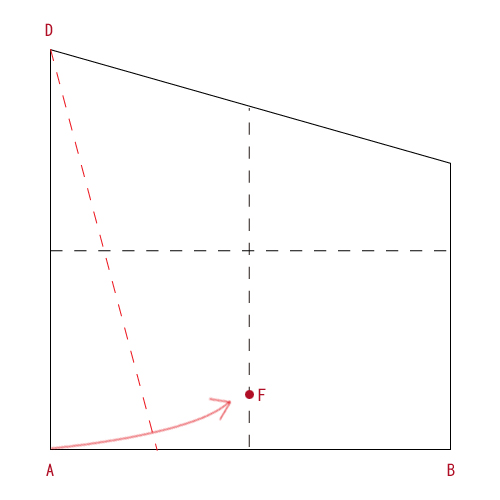
- 最後に、図の破線部分を山折して完成!

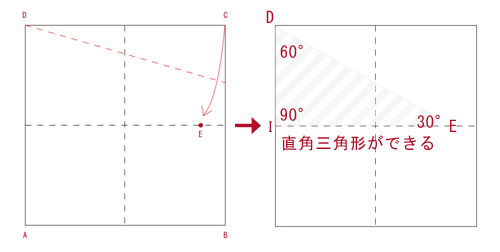
直角三角形の斜辺の長さは横の辺の長さの2倍です。これを用いて作図しました。以下は詳しい証明になります。
手順2で、頂点Cを横断上(点Eの位置)に重ねました。この時、新たな直角三角形DEIが生まれます。DC=DEであり、DE=2DIであることより、角度DEIは60度となる。角EFCは30度となります。
線分DIIは角の二等分線であることから角IIDEは15度となります。
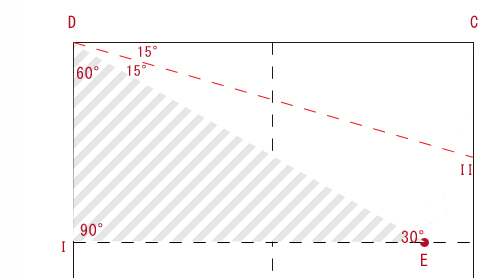
次に手順3の図を思い出してください。手順2と同様に頂点Dを軸として縦断線上に折りました。
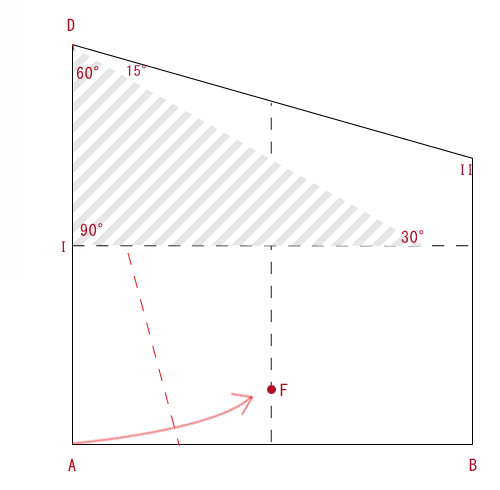
対称性から線分DIIとDIIIは等しい。よって二等辺三角形であることがわかります。更に頂点Dはこれまで求めてきた結果から60度と分かりますね。
他二つの角度の合計は180度-60度=120度
二等辺三角形なので、二つの角度は同じ=60度
よって三つの角度は60度の正三角形だと分かります。
実際に折ったものはこちら。作品としての見栄えはあれですけど・・

参考文献
折紙の数学―ユークリッドの作図法を超えて
内接する最大の正三角形の他にも正五角形~十九角形まで紹介されています。数学本なので、もちろん証明式も掲載。作品や折り紙遊びというよりは、数学的に可能な事を証明している感じです。
60度定規の作り方
上記正三角形で60度を作る事が出来るのですが、毎回正三角形を作るわけにはいきません。そこで、オリガミクスという本に紹介されていた60度定規の作り方をご紹介します。
- 正方形の紙を縦に四つ折りにします。
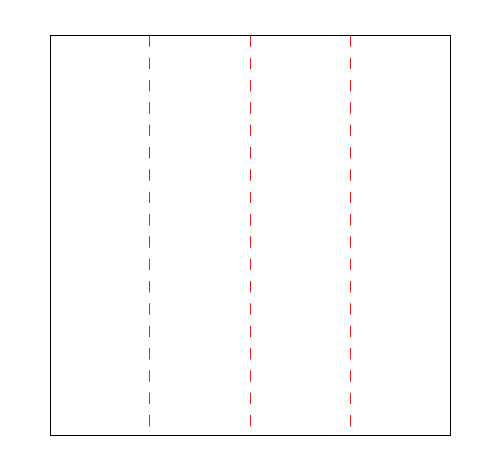
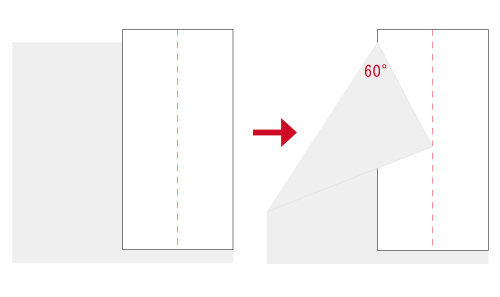
- 60度を作りたい同じ大きさの紙を下に引いて図のように折ります。
参考文献
オリガミクス〈1〉幾何図形折り紙
こちらの芳賀先生の五箇条に「仕上がりは芸術的でなければならない」とあり、数学的でありながら作品として魅せる折り方が多数掲載されています。もちろん証明式もあります。下の写真の直角三角形と、ダビデの星はこの本に紹介されていた方法で作りました。右の内接する最大の正八角形は「折り紙の数学」に紹介されていたものです。
角度を意識すると1枚の紙から色んなものが生み出せますね。

折り紙の白銀比・黄金比
正方形の一片と対角線の比は1:√2、つまり白銀比です。この白銀比を含んだ折り紙から、正五角形を作る事によって黄金比を生み出すことが可能です。少し難しいですが、五点星も作る事ができます。
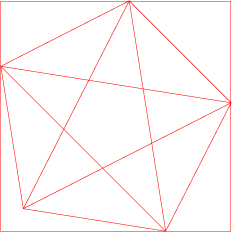
展開図の幾何学模様
折り紙は直線・対称性の性質を含んでいるので、その展開図もとても幾何学的です。
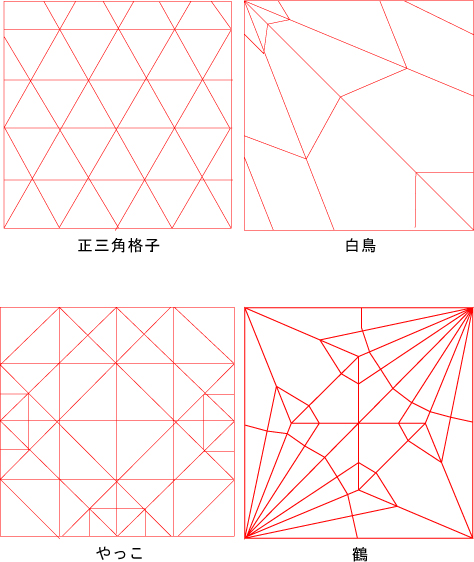
折り紙の展開図って面白いなーと改めて思ったのでご紹介します。正三角格子(正四面体などの立体を折る時につける折り目)、白鳥、やっこ、鶴の展開図を紹介します。直線と角度を意識して作図すると、より美しい模様が作れそうです。
正三角格子はパターンとして使用できそうですね。
折り紙の展開図を作成するフリーソフトもあります。
自作の展開図を作りたいかたはこちらをどうぞ。※Javaが動作する環境が必要です。
折紙展開図エディタ ORIPA
 Japanese style web design いろはクロス
Japanese style web design いろはクロス


コメントを残す